FUNDAMENTOS DE LA ENSEÑANZA APRENDIZAJE
DE LAS MATEMÁTICAS PARA MAESTROS
CAPÍTULO I: PERSPECTIVA EDUCATIVA DE LAS
MATEMÁTICAS
1. Establecer relaciones y
diferencias entre la concepción idealista platónica y la concepción
constructivista.
|
concepción
idealista platónica
|
concepción
constructivista
|
|
·
El alumno debe adquirir primero las estructuras
matemáticas de forma axiomática.
·
La matemática es una ciencia autónoma.
·
El currículo es sencillo, no se preocupa por sus
aplicaciones a otras ciencias.
|
·
Las aplicaciones tanto internas como externas, deben
preceder y seguir a la creación de las matemáticas.
·
La matemática es una ciencia multidisciplinar.
·
El currículo es complejo, porque requiere de
conocimientos de otras áreas.
|
|
·
Ambas siguen la construcción de un conocimiento
matemático.
|
|
2. ¿Cuáles son los fines de
las matemáticas en relación a la sociedad?
Su
fin primordial es formar ciudadanos cultos.
·
Que los alumnos lleguen a comprender y a
apreciar el papel de las matemáticas en la sociedad, incluyendo sus diferentes
campos de aplicación y su contribución en su desarrollo.
·
Que los alumnos lleguen a comprender y a
valorar el método matemático, la clase de preguntas que un uso inteligente de
las matemáticas permite responder.
3.
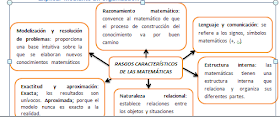
¿Cuáles son los rasgos característicos de las matemáticas? Explicar mediante un organizador.
¿Cuáles son los rasgos característicos de las matemáticas? Explicar mediante un organizador.
4. ¿Cuáles son los tipos de
objetos que intervienen en la actividad matemática? Ejemplificar.
|
. Mediante un organizador,
explicar los procesos matemáticos que intervienen en la actividad matemática.
| |||
6. Definir e identificar
Transposición Didáctica.
La transposición
didáctica hace referencia al cambio que el conocimiento matemático sufre para
ser adaptado como objeto de enseñanza.
El contenido
matemático debe ser adaptado a la edad y conocimiento del alumno.
Por ejemplo:
En términos formales, la suma es una
operación aritmética definida sobre conjuntos de números (naturales, enteros,
racionales, reales y complejos) y también sobre estructuras asociadas a ellos,
como espacios vectoriales con vectores cuyas componentes sean estos números o
funciones que tengan su imagen en ellos. No es lo mismo que decir; la suma es
la operación matemática de combinar o añadir dos números para obtener una
cantidad final o total. O la suma es el proceso de juntar dos colecciones de
objetos con el fin de obtener una sola colección.


No hay comentarios:
Publicar un comentario