2.-
¿CUÁLES SON LAS RELACIONES Y DIFERENCIA ENTRE EDUCACIÓN Y DIDÁCTICA DE LA
MATEMÁTICA?
3.-
¿CUÁL SON LAS RELACIONES QUE SE ESTABLECEN EN EL MODELO DE STEINER?
4.-
¿CUÁL SON LAS RELACIONES QUE SE ESTABLECEN N EL MODELO DE HIGGINSON?
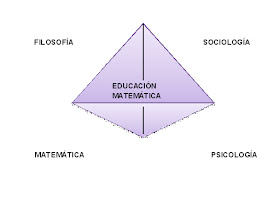
HIGGINSON
considera ala matemática, psicología, sociología y filosofía como las cuatro
disciplinas fundamentales de la Educación
Matemática.
Estas
distintas dimensiones de la Educación Matemática asumen las preguntas
básicas que se plantean en nuestro
campo:
ü Qué
enseñar (matemática)
ü Por
qué (filosofía)
ü A
quién enseñar (sociología)
ü Cuando
y cómo ( psicología)
5.-
¿QUÉ PERMITE UN BUEN MARCO TEÓRICO EN EL CAMPO DE LA MATEMÁTICA?
Un
marco teórico permite sistematizar los conocimientos dentro de una disciplina,
lo que constituye un primer paso para conseguir una visión clara de la unidad
que pueda existir en nuestras percepciones. La teorización es un requisito para
que un área de conocimiento alcance la categoría científica y pueda desempeñar su papel explicativo y
predictivo de fenómenos: puede decirse que la investigación científica
significativa está siempre guiada por una teoría, aunque veces lo sea de un
modo implícito.
6.-
¿CUÁLES SON LOS SENTIDOSSEMÁNTICOS DEL TÉRMINO TEORÍA SEGÚN NAGEL?
Son
4 sentidos para el término teoría:
·
Una teoría es un sistema de enunciados,
frecuentemente universales y relativos a
distintos aspectos de fenómenos complejos, capaces de explicar algunas
regularidades empíricamente establecidas partir de sucesos observados y, en
muchos casos, de predecir con distintos grados de precisión cierta clase de
ocurrencias individuales.
·
El 2º sentido de teoría se refiere a “una ley
o generalización que afirma alguna relación de dependencia entre variables” que
puede adoptar una forma estrictamente universal o tener un alcance estadístico.
·
El 3º sentido se refiere al a identificación
de “una clase de factores o variables que por distintas razones se suponen
constituyen los determinantes principales los fenómenos que se investigan en
una disciplina determinada.
·
El 4º sentido atribuido por Nagel a una
teoría se refiere a cualquier análisis más o menos sistemático de un conjunto
de conceptos relacionados.
7.-
¿CUÁL ES LA RELACIÓN Y DIFERENCIA ENTRE TEORÍA FENOMENOLÓGICAS Y FUNDAMENTALES?
Burkhardt (1988)
hace una distinción interesante entre las teorías que denomina fenomenológicas
y teorías fundamentales.
8.-
¿CUÁLES SON LOS COMPONENTES BÁSICOS EN LOS PROCESOS DE CONSTRUCIÓN DE TEORÍA?
9.-
¿CUÁL SON LAS CORRIENTES EPISTEMOLÓGICAS QUE AYUDAN A EXPLICAR OBJETO Y MÈTODO
DE LA DIDÁCTICA DE LA MATEMÁTICA?
·
Didáctica general
·
Pedagogía
·
Psicología
10.-
¿CUÁL SON LAS CARACTERÍSTICAS (COMPONENTES) QUE DEFINEN UN CAMPO DE
CONOCIMIENTO SEGÚN MARIO BUNGE?
Para
dicho autor un campo de conocimiento puede caracterizarse como un sector de la
actividad humana dirigido a obtener, difundir o utilizar conocimientos de
alguna clase. Las características que definen los campos de conocimiento las
simboliza del siguiente modo:
C= C,SS,D,G,F,E,P,A,O,M
C: comunidad de
científicos que cultivan C
S: sociedad
D: dominio o universo
del discurso (los objetos de estudio)
G: concepción general o
filosófica inherente
F: fondo formal
(conjunto de herramientas lógicas o matemáticas utilizables)
E: fondo específico o
conjunto de supuestos que toma de oros campos.
P: problemática, o
colección de problemas abordables.
A: fondo específico de
conocimientos acumulados
O: objetivos de metas
M: metódica o conjunto
de métodos utilizables.
11.-
¿CUÁLES SON LOS PRINCIPALES LÍNEAS DE LA INVESTIGACIÓN EN LA DIDÁCTICA DE LA
MATEMÁTICA?
·
Complementarias
·
En competencia
·
Originales
·
Revolucionarias o contrarrevolucionarias
12.-
¿CUÀLES SON LOS COMPONENTES DEL PROGRAMA DE INVESTIGACIÓN DEL GRUPO TEM?
En este programa se
distinguen 3 componentes:
·
La identificación y formulación de los
problemas básicos en orientación, fundamento, metodología y organización de la
educación matemática como una disciplina.
·
El desarrollo de una aproximación comprensiva
ala educación matemática, que debe ser vista en su totalidad como un sistema
interactivo, comprendiendo investigación, desarrollo y práctica.
·
La organización de la investigación sobre la
propia educación matemática como disciplina que, por una parte , proporcione
información y datos sobre la situación, los problemas y las necesidades de la
misma, teniendo en cuenta las diferencias nacionales y regionales y, por otra
contribuya al desarrollo de una meta-o-reflexiva como base para el
establecimiento y realización de los programas de desarrollo del TEM.
13.-
¿QUÉ ASPECTOS SE ABORDAN EN LA 2º CONFERENCIA DEL TEM ANÑO 1985?
Se
centro sobre el tema genérico “Fundamento y Metodología de la disciplina
Educación Matemática”, la mayoría de las contribuciones resaltó el papel de la
teoría y la teorización en dominios particulares. En estos temas figuran:
ü Teoría
sobre la enseñanza
ü Teoría
de las situaciones didácticas
ü Teoría
interaccionista del aprendizaje y la enseñanza
ü El
papel de las metáforas en teoría del desarrollo
ü El
papel de las teorías empíricas en la enseñanza dela matemática
ü La
importancia de las teorías fundamentales matemáticas
ü Conceptos
teóricos para la enseñanza de la matemática aplicada
ü La
teoría de la representación como base para comprender el aprendizaje matemático
ü Estudio
históricos sobre el desarrollo teórico de la educación matemática como una
disciplina.
14.-
¿QUÉ ASPECTOS SE ABORADARON EN LA 3º CONFERENCIA DEL TEM?
ü El desfase
entre investigación sobre la enseñanza-aprendizaje ene el proceso real en las
clases de matemáticas como un fenómeno tradicional y como un problema presente
crucial.
ü El
desfase entre investigación sobre la enseñanza e investigación sobre el aprendizaje.
ü Modelos
para el diseño de la enseñanza a la luz de la investigación sobre el
aprendizaje.
ü La
necesidad de la teoría y la investigación en trabajos y proyectos de desarrollo
y su posición en el contexto de investigación sobre enseñanza-aprendizaje.
ü El papel del contenido, la orientación del
área temática y las distintas perspectivas de la matemáticas en el estudio y
solución del desfase investigación-aprendizaje y el desarrollo de modelos
integradores.
ü El
desfase enseñanza-aprendizaje a la luz de los estudios sobre procesos i
interacción social en la clase.
ü Implicaciones
del tema de la conferencia sobre la formación de profesores.
ü El
ordenador como una tercera componente en la interacción enseñanza-aprendizaje.
15.-
¿QUÉ TEMAS SE TRATARON EN LA 4º CONFERENCIA?
Son
los siguientes:
ü Relaciones
entre las orientaciones teóricas y los métodos de investigación empírica en
educación matemática.
ü El
papel de los aspectos y acercamientos holísticos y sistémicos en educación
matemática.
16.-
¿QUÉ TEMAS SE TRATARON EN LA 5º CONFERENCIA?
Son
los siguientes:
ü El
papel de las metáforas y metonimias en matemáticas, educación matemática y en
la clase de las matemáticas.
ü Interacción
social y desarrollo del conocimiento. Perspectiva de Vygotsky sobre la
enseñanza y el aprendizaje matemático en la zona de construcción.
17.-
¿QUÉ ESTUDIA LA PSICOLOGÍA DE LA EDUCACIÓN?
Estudia
científicamente los procesos de enseñanza aprendizaje, así como de los
problemas que en el contexto de los mismos puedan presentarse.
18.-
¿CUÁLES SON LOS OBJETIVOS DEL GRUPO PEM?
Son
los siguientes:
ü Promover
contactos internacionales en intercambio de información científica sobre la
Psicología de la Educación Matemática.
ü Promover
y estimular investigación interdisciplinar en esta área con la cooperación de
psicólogos, matemáticos y profesores de matemáticas.
ü Fomentar
una comprensión más profunda y correcta de los aspectos psicológicos de la enseñanza
y aprendizaje de la matemática.
19.-
¿QUÉ FENÓMENOS ANALIZA VERGNAUD DE UNA PERPECTIVA PSICOLÓGICA?
Son
4 fenómenos:
ü La
organización jerárquica de las competencias y concepciones de los estudiantes.
ü La
evolución a corto plazo de las concepciones y competencias en el aula.
ü Las
interacciones sociales y los fenómenos inconscientes.
ü La
identificación de teoremas en acto, esquemas y símbolos.
20.-
¿QUÉ ASPECTOS DESTACA BALACHEF?
Entre
los que destaca tenemos:
ü La
especificidad del conocimiento matemático. La investigación sobre el
aprendizaje del álgebra, geometría, o el cálculo no se puede desarrollar sin un
análisis epistemológico profundo de los conceptos considerados como nociones
matemáticos.
ü La
dimensión social. Tanto el estatuto social del conocimiento que se debe
aprender como el papel crucial de las interacciones sociales en el proceso de
enseñanza requieren una consideración importante de la dimensión social de la
investigación.
21.-
¿QUÉ PLANTEA LA PERSPECTIVA CONTRUCTIVISTA SOBRE EL APRENDIZAJE MATEMÁTICO?
De
los estudios cognitivos se deduce uno de los supuestos básicos subyacentes de
la investigación actual sobre aprendizaje. Consiste en aceptar que el niño
construye, de un modo activo, el conocimiento a través de la interacción con el
medio y la organización de sus propios constructos mentales. Aunque la instrucción afecta claramente a lo que el
niño aprende, no determina tal aprendizaje. El niño no es un receptor pasivo
del conocimiento; lo interpreta, lo estructura y lo asimila a la luz de sus
propios esquemas mentales.
22.-
¿QUÉ PLANTEA LA PERPECTIVA DEL PROCESAMIENTO DE INFORMACIÓN?
El
campo de la ciencia cognitiva intenta capitalizar el potencial de la metáfora
que asemeja el funcionamiento de la mente a un ordenador para comprender el
funcionamiento de la cognición como procesamiento de la información, y como
consecuencia comprender los procesos de enseñanza y aprendizaje. Se considera que el cerebro y
la mente están vinculados como el ordenador y el programa
23.-
¿CUÁL SON LOS PLANTEAMIENTOS DE LA CONCEPCIÓN FUNDAMENTAL DE LA DIDÁCTICA DE LA
MATEMÁTICA?
Interés
por establecer un marco teórico original, desarrollando sus propios conceptos y
métodos y considerando las situaciones de enseñanza-aprendizaje globalmente.
Los modelos desarrollados comprenden las dimensiones epistemológicas, sociales
y cognitivas y tratan de tener en cuenta la complejidad de las interacciones
entre el saber, los alumnos y el profesor, dentro del contexto particular de la
clase.
24.-
¿QUÉ PLANTAE EL ENFOQUE SISTÉMICO DE LA DIDÁCTICA DE LA MATEMÁTICA?
Las
didácticas que comparten esta concepción de la didáctica relacionan todos los
aspectos de su actividad con las matemáticas. Se argumentan, para basar ese
enfoque, que el estudio de las transformaciones de la matemática, bien sea
desde el punto de vista de la investigación o de la enseñanza siempre ha
formado parte de la actividad del matemático, de igual modo que la búsqueda de
problemas y situaciones que requiera para su solución una noción matemática o
un teorema.
25.-
¿QUÉ PLANTEA LA TEORÍA DE SITUACIONES DIDÁCTICAS?
En
esta teoría se adopta una perspectiva piagetiana, en el sentido de que se
postula que todo conocimiento se construye por interacción constante entre el
sujeto y el objeto, pero se distingue de otras teorías constructivistas por su
modo de afrontar las relaciones entre el alumno y el saber. Los contenidos son
el substrato sobre el cual se va a desarrollar la jerarquización de estructuras
mentales.
26.-
¿COMO SE EXPLICA LA RELACIÓN ENTRE OBSTÁCULOS Y APRENDIZAJES MATEMÁTICOS?
Un
obstáculo es una concepción que ha sido en principio eficiente
par resolver algún tipo de problemas pero que falta cuando se aplica a
otro. Debido a su éxito previo se
resiste a ser modificado o a ser
rechazado: bien a ser una barrera para un aprendizaje posterior. Se releva por
medio de los errores específicos que son constantes y resistentes. Para superar
tales obstáculos se precisa situaciones didácticas diseñadas para hacer a los
alumnos conscientes de la necesidad de cambiar sus concepciones y para
ayudarles en conseguirlo.
27.-
¿COMÓ SE EXPLICA LA RELACIÓN CON EL SABER?
El
problema central de la didáctica es par este autor el estudio de la relación
institucional con el saber, de sus condiciones y de sus efectos. El estudio de
la relación personal es en la práctica fundamental, pero epistemológicamente
secundario. Este programa, sin embargo, no puede tener éxito sin una toma en
consideración del conjunto de condicionantes del alumno, que juegan o pueden
jugar un papel en la formación de su relación personal con el objeto de saber
en cuestión.
28.-
¿CÓMO SE EXPLICA LA TRANSPOSICIÓN DIDÁCTICA?
La
relatividad del saber a la institución en que se presenta lleva al concepto de
transposición didáctica. La transformación se pasa del saber matemático al
saber de enseñar. Se pasa de la descripción de los empleos de la noción a la
descripción de la misma de la misma
noción y la economía que supone par la organización del saber.
29.-
¿CÓMO SE EXPLICA EL CONTRATO DIDÁCTICO Y LOS CAMPOS CONCEPTUALES?
El contrato didáctico es
un conjunto de reglas – con frecuencia no anunciadas implícitamente – que
organizan las relaciones entre el contenido enseñado, los alumnos y el profesor
dentro de la clase de matemáticas.
Campos conceptuales: los
conceptos matemáticos se dotan de significado a partir de una variedad de
situaciones: cada situación no puede ser analizada usualmente con la ayuda de
un solo concepto sino que precisa varios de ellos.
30.-
¿CÓMO SE EXPLICA EL CARÁCTER AUTÓNOMO, PLURIDISCIPLINAR Y TRANDISCIPLINAR DE LA
DIDÁCTICA DE LA MATEMÁTICA?
Carácter autónomo: tiende
a integrar todos los sentidos precedentes y a asignarles un lugar en relación a
una teoría unificadora del hecho didáctico, cuya fundamentación y métodos
serían específicos, pretendiendo una justificación endógena.
Pluridisciplinar: aparece
como una etiqueta cómoda para designar
las enseñanzas necesarias para la formación técnica y profesional de los
profesores.
Transdisciplinar: es
la que cubre no solo las interacciones o reciprocidades entre proyectos de investigación
especializados, sino la que sitúa estas relaciones dentro de un sistema total
de límites fijos entre disciplinas.
31.- RELACIÓN DE LOS MÓDELOS DE: STEINER
Y HIGGINSON






No hay comentarios:
Publicar un comentario