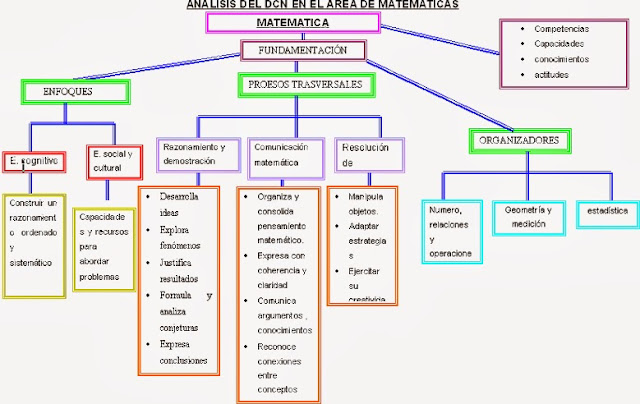
¿Qué son competencias y cómo se estructura?
Una competencia es
Habilidad, destreza, Ser capaz de hacer algo al término del proceso educativo y
haber desarrollado los procedimientos para continuar aprendiendo de forma
autónoma a lo largo de la vida.
Estructura:
1)
Verbo + contenido.+ condición++ contexto+valor
Organizador
|
competencias
|
interpretación
|
ejemplos
|
Números, relaciones y operaciones
|
Resuelve
problemas de contexto real y contexto
matemático que requiere del establecimientos de relaciones y contextual con
números contextual y fracciones e interpreta los resultados demostrando
perseverancia en la contextual de soluciones.
|
Resuelve
problemas de su contexto real y matemático haciendo uso de las cuatro
contextual básicas y fracciones de los números contextual, relacionándolos
con los objetos contextual a los estudiante, en donde este se mostrara
interesado por dar solución a dicho problema.
|
-
El total de alumnos en aula( niños +
niñas)
-
Total de naranjas que le queda si
regala cierta cantidad de naranjas.
-
El total de cosecha de un
determinado producto dividida entre cierto numero de personas.
|
Geometría y medición
|
Resuelve y formula problemas demostrando
perseverancia y actitud exploratoria cuya solución requerirá de relaciones
entre los elementos de polígonos
regulares y sus medidas: áreas, perímetros,
e interpreta sus resultados y
los comunica utilizando el lenguaje matemático.
|
Resuelve y plantea problemas, de medida, tanto de
áreas como perímetros, utilizando elementos contextual a su realidad
contextual, demostrando perseverancia y actitud para resolver dichos
problemas.
|
-
el área de una chacra de un
estudiante.
-
el perímetro de aula. Ventanas ,
mesa, la puerta del aula como también puede ser de la casa del niño.
-
El área o perímetro de su cuaderno.
Libro, etc.
|
Estadística
|
Resuelve
problemas con datos estadísticos y su entorno y comunica con precisión la
información obtenida mediante tablas y gráficos.
|
Resuelve
problemas con datos estadísticos, con relación a su contexto cultural y familiar,
comunica con precisión mediante tablas y graficaos
.
|
-
El numero de habitantes de la comunidad del
estudiante(niños, jóvenes, ancianos)
-
el numero de alumnos del colegio del e
estudiante.( por edad, numero de varones, numero de mujeres, etc.
|
¿Qué es una capacidad y como se
estructura.?
La capacidad es una aptitud o suficiencia para hacer algo
al término del proceso educativo y seguir adquiriendo conocimientos para
aplicarlos en la vida cotidiana
Existen tres tipos de competencias según el D.C.N:
Capacidades
fundamentales. Se caracterizan por su alto grado de complejidad. Ellas son el
pensamiento creativo, el pensamiento crítico, la toma de decisiones y la
solución de problemas
Capacidades de
área. Son una concreción de las capacidades fundamentales, una adaptación de
las capacidades al área curricular de que se trate.
Capacidades
específicas. Son las menos complejas, se traducen en actividades que el profesor
trabaja con sus alumnos y sirven para obtener un resultado expresado en logros
de aprendizaje. La relación entre las capacidades específicas y de área es muy
estrecha. Por ejemplo, identifica, retiene, compara, contrasta, relaciona,
jerarquiza, organiza, sintetiza, interpreta, infiere, extrapola, argumenta,
planifica
Estructura
1) verbo + contenido
capacidades del 3º y 4º grado según el
D.C.N
|
Tercer
grado
|
Organizador
|
competencias
|
Numero, relaciones y operaciones
|
Razonamiento y
demostración
·
Reconoce
la relación “mayor que”, “menor que”, igual que” y ordena números de hasta
cuatro cifras.
·
Reconoce
fracciones homogéneas y las compara estableciendo relaciones “mayor que”,
“menor que”, “igual que” relacionada a proyectos productivos.
·
Representa
la adición y sustracción de fracciones Homogéneas relacionada a proyectos
productivos.
·
Opera el producto de un número de dos
dígitos por otro de un dígito.
·
Opera y representa la división exacta de
números naturales relacionados a su entorno.
·
Identifica patrones matemáticos de adición,
sustracción y multiplicación de números, con uso de la calculadora u otro
recurso de las TIC, y tecnología nativa.
·
Formula sucesiones de razón aritmética con
números naturales
Comunicación Matemática
·
Grafica
fracciones relacionada a proyectos productivos.
Resolución de problemas
·
Resuelve
problemas de adicción y sustracción con números naturales de hasta cuatro
cifras relacionada a proyectos productivos.
·
Resuelve
y formula problemas de adicción y sustracción de fracciones homogéneas
|
Geometría y medición
|
Razonamiento y
demostración
- Identifica
rectas paralelas y perpendiculares en cuerpos geométricos: cubo, prisma,
cilindro, utilizando objetos de
su contexto.
- Interpreta
y representa la equivalencia de minutos, horas, días y semanas
Comunicación matemática.
- Resuelve
problemas sobre la duración de un acontecimiento, relacionado a su
contexto.
Resolución de problemas.
- Mide
superficies y perímetros de objetos relacionados a su entorno haciendo
uso de diferentes unidades.
·
Resuelve problemas
que implican calculo de perímetros, áreas de figuras geométricas básicas, relacionadas a su
contexto.
|
|
Estadística
|
Razonamiento y demostración
·
Interpreta y
representa información numérica en tablas de doble entrada.
Comunicación
matemática
- Representa
información mediante tablas de doble entrada, gráficos, y barreras
pictogramas, utilizando elementos familiares a su entorno.
Resolución
de problemas.
- Resuelve
gráficos de barreras y pictogramas en relación a su medio.
|
|
|
Cuarto grado
|
organizadores
|
competencias
|
Numero, relaciones y operaciones
|
Razonamiento
y demostración
·
Reconoce
la relación “mayor que”, “menor que”, igual que” y ordena números de hasta
cuatro cifras.
·
Interpreta
y compara números decimales hasta el orden de la décima
·
Identifica
patrones matemáticos de adición, sustracción y multiplicación de números, con
uso de la calculadora u otro recurso de las TIC, y tecnología nativa.
·
Interpreta
operaciones de razonamiento lógico matemático en situaciones problemáticas de
su entorno hasta de tres cifras.
Comunicación matemática
·
Grafica
fracciones tanto equivalentes como heterogéneas relacionadas a proyectos productivos.
·
Establece
relaciones entre cantidades directamente proporcionales y las organiza en
tablas
Resolución
de problemas
·
Resuelve
problemas de adicción y sustracción con números decimales y fracciones de proyectos
productivos.
·
Resuelve
y formula problemas de adicción y sustracción de fracciones homogéneas
|
Geometría y medición
|
Razonamiento y demostración
·
Interpreta la
ubicación de figuras geométricas planas en el primer cuadrante del plano cartesiano.
·
Identifica rectas
paralelas secantes , en relación a su
entorno
Comunicación
matemática
·
Grafica figuras
simétricas planas respecto a su contexto.
·
Grafica polígonos
en el plano cartesiano e identifica sus lados y ángulos
·
Mide clasifica
ángulos en relación a su entorno.
·
Mide capacidad de
recipientes, en litros y mililitros utilizando materiales de su contexto
·
Argumenta la
relación entre áreas y el perímetro de un polígono: rectángulo,
cuadrado, figuras compuestas en
relación a su contexto
Resolución de problemas.
·
Resuelve y formula
problemas que requieren diferentes unidades de medición
·
Resuelve problemas
que implican cálculo de áreas de rectángulos cuadrados, y figuras compuestas
relacionándolos con su contexto.
|
Estadística
|
Razonamiento y demostración
·
Interpreta y elabora tablas de doble
entrada, gráficos líneas y pictogramas en relación a situaciones cotidianas
Comunicación matemática
- Formula y
argumenta la posibilidad de ocurrencia de sucesos numéricos y no
numéricos: seguros, probables, improbables de situaciones cotidianas.
Resolución de problemas
- Resuelve
problemas y los representa
mediante tablas de doble entrada, gráficos líneas y pictogramas en
relación a situaciones cotidianas
|
¿Qué conocimientos se
desarrollara (3ero y 4to grado) según el D.C.N.?
Los conocimientos son los contenidos que se
desarrollaran en proceso de enseñanza- aprendizaje, los cuales aumentaran de
nivel de acuerdo al grado en que serán aplicados.
Para poder adquirir los siguientes conocimientos
propuestos en el cuadro, deben ser desarrollados, de acuerdo al contexto del
estudiante para que así sea posible lograr un aprendizaje significativo.
Los conocimientos que se desarrollan en el área de
matemáticas en los grados de 3ero y 4to grado de primaria de acuerdo al D.C.N
son los siguientes:
Grado
|
organizador
|
conocimientos
|
3er
grado
|
Numero, relaciones y operaciones
|
- Valor
de posición en números de hasta cuatro cifras.
- Relación
de orden en números naturales de hasta cuatro cifras.
- Adición
y sustracción de números con resultados de hasta cuatro cifras.
- Fracciones
de conjuntos de objetos y de cantidades continuas.
- Fracciones
usuales: 1/2; 1/4 y 1/8
- Fracciones
homogéneas.
- Relación
de orden en fracciones homogéneas.
- Fracciones
equivalentes.
- Adición y sustracción de fracciones
homogéneas.
- Multiplicación de un número de un solo
dígito por 10
- .Multiplicación
de un número de dos dígitos por otro de un dígito.
- Doble,
triple, cuádruplo.
- Significado
de la división exacta: resta sucesiva y reparto.
- Operaciones
combinadas de adición, sustracción, multiplicación y división con
números de hasta cuatro cifras.
- Sucesiones
de razón aritmética.
- Equivalencias
y canjes de monedas soles y céntimos) y billetes de hasta S/. 200
|
Geometría
y medición
|
- Rectas
paralelas y perpendiculares en cuerpos geométricos.
- Eje
de simetría de figuras simétricas planas.
- Desplazamiento
de objetos con referentes de ejes, cruces, filas, columnas, cuadrantes.
- Volumen:
Capacidad de unidades arbitrarias.
- Áreas
de figuras geométricas en unidades arbitrarias.
- Perímetro
de figuras geométricas básicas: cuadrado, rectángulo, triángulos, en
metros, centímetros, milímetros.
- Referentes
temporales: minutos, horas, días, semanas.
|
Estadística
|
- Tablas
de doble entrada, gráfico de barras y pictogramas.
- Sucesos
numéricos y no numéricos: seguros, probables e improbables.
|
4to grado
|
Numero, relaciones y operaciones
|
- Descomposición
polinómica de un número natural.
- Números decimales con
aproximación a la décima.
- Ordenamiento
de números naturales de hasta cuatro cifras.
- Operaciones
combinadas con números naturales.
- Aproximaciones
a la decena, centena o millar más cercano en el cálculo con números.
- División
de números de hasta tres cifras.
- Fracciones
equivalentes.
- Fracciones
heterogéneas.
- Operaciones
combinadas de adición, sustracción, multiplicación y división de números
naturales de hasta tres cifras.
- Adición
y sustracción de números decimales con una cifra decimal.
- Adición
y sustracción de fracciones heterogéneas, con denominadores 2, 4, 5, 8,
10.
- Adición y sustracción de fracciones y
números decimales.
- Multiplicación
de un número natural por 10; 100.
- Sucesiones
con números naturales.
- Referentes
temporales: segundos, minutos, horas, días, semanas.
- Equivalencias
y canjes con monedas y billetes.
- Tablas de proporcionalidad directa.
|
|
Geometría y medición
|
- Figuras
geométricas en el plano cartesiano.
- Rectas
secantes y paralelas.
- Ángulos:
Llano, recto, obtuso, agudo.
- Vértices,
caras, aristas, en el cubo, prisma recto de base poligonal.
- Transformaciones
en el plano: simetría de figuras respecto a un eje; traslación de
figuras geométricas.
- Polígonos:
lados y ángulos.
- Capacidad
en litros y mililitros.
- Unidades
para medir m, cm, mm
- Unidades
para medir superficie: cm ó mm.
- Superficie
de figuras geométricas: cuadrado, rectángulo, triángulo.
- Área
y perímetro de un polígono.
|
Estadística
|
- Tablas
de doble entrada.
- Gráfico
de barras, pictogramas y gráfico de líneas.
- Sucesos
numéricos y no numéricos: probables e improbables.
|
¿ Qué métodos se
utiliza para desarrollar dichos procesos ya vistos anteriormente
- Método deductivo e inductivo
- Método experimental
- Método axiomático.
- Método científico
¿ Cómo evaluar el área de matemática de acuerdo al D.C.N(3ero y 4to)
?
el alumno será evaluado de acuerdo como
desarrolle o despeñe las siguientes actitudes. la evaluación es
literal y comprende una escala de calificación basada en cuatro valores: C, B,
A y AD. El alumno logra la competencia cuando obtiene el calificativo AD.
Actitudes
|
- Muestra
predisposición y curiosidad por el uso del lenguaje simbólico y gráfico
a partir de patrones.
- Muestra autonomía y
seguridad al resolver problemas y comunicarlos.
- Disfruta y comparte
sus logros al resolver diversos problemas matemáticos.
- Muestra interés por
comunicar información utilizando lenguaje matemático y gráfico.
- Comparte con los
demás expresiones matemáticas usuales de su contexto.
- Es creativo al
desarrollar ejercicios matemáticos.
- Aprecia el valor de
la matemática y su uso en la vida cotidiana.
- Colabora con los
estudiantes que presentan Necesidades Especiales y demás, en la
resolución de problemas matemáticos
|
C
|
Cuando
el alumno requiere de ayuda constante del docente para el desarrollo del
aprendizaje.
|
B
|
Cuando el
alumno desarrolla las actitudes con ayuda porque tiene dificultades.
|
A
|
Cuando el alumno logra desarrolla las actitudes
pero no lo aplica con facilidad en la vida diaria
|
AD
|
Cuando
el alumno desarrolla todas las actitudes previstas en el cuadro y lo aplica
en la vida diaria
|